Personal & Professional Biography
Andrew has taught Algebra I, Advanced Algebra with Trigonometry & IB Math Studies SL at Prosser Career Academy, a Chicago Public High School, for the past 10 years. His most rewarding professional development experiences include National Board Certification, OneGoal & the Michigan State-Wipro STEM Fellowship. He has a passion for teaching students how to become better problem solvers and enjoys tackling tough problems himself.
Andrew and his lovely wife Nimisha, married for two years, are expecting their first child (!) in December. In his free time, Andrew enjoys training for triathlons, marathons, and open water swims. Also, he has a wanderlust. Thailand, South Africa, Peru, Guatemala and Montana are among his favorite places on earth.
Andrew and his lovely wife Nimisha, married for two years, are expecting their first child (!) in December. In his free time, Andrew enjoys training for triathlons, marathons, and open water swims. Also, he has a wanderlust. Thailand, South Africa, Peru, Guatemala and Montana are among his favorite places on earth.
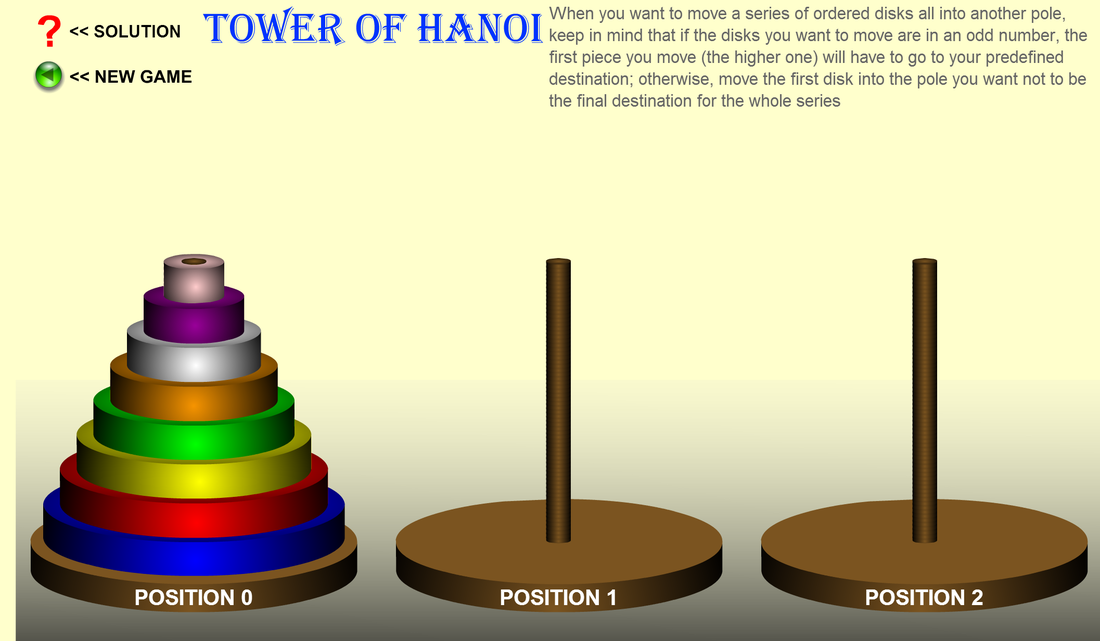
Amazing Teaching Moment: Behold, the Tower of Hanoi!
Taken from http://britton.disted.camosun.bc.ca/hanoi.swf
I was first introduced to the Tower of Hanoi in my DePaul University grad school class almost a decade ago. Immediately, I was hooked by the elegance and complexity of the problem. Sixty-four disks lie on Pole A and, in the minimum number of moves possible, must be moved to Pole C (Pole B lies between A and C). To solve the problem, you are required to move the 64 disks while following two rules: you must move one disk only at a time onto Poles A, B or C and can never place a larger disk upon a smaller one. What is the minimum number of moves required to solve this problem?
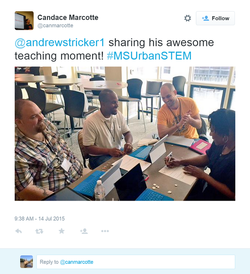
Students used pennies, nickels, dimes and quarters to replicate the Tower of Hanoi. First, they started by solving an easier problem. What if, instead of 64 disks, there was only one disk? How many moves would be required to solve the problem? What if there were two disks? Three disks? From there, students saw patterns, formulated hypotheses, and tested their ideas.
They enjoyed the hands-on nature of the problem and appreciated the challenge of deriving an explicit formula to model the minimum number of moves to solve the Tower. They were curious as to whether there are extensions to the Tower (there are). Someone suggested that students create their own Tower extensions based on certain conditions (e.g. the Adjacency Requirement and double the original number of disks). Another Fellow saw how this problem could be modified for her students. A STEM coach, who knew of the problem prior to today, appreciated the problem solving approach using the coins, trial-and-error, patterns in the numbers and teamwork.
The Tower of Hanoi is the capstone activity of our Exponents unit. On day one of the Tower, students investigate a variation of the famous Wheat and Chessboard fable. On day two, they read the history of the Tower and attempt to solve it. Students are astounded by the number of years it would take, moving one disk per one second, to solve the Tower by hand. Day three offers extensions to the problem, including the Adjacency Requirement and Double Tower. Past students have told me that this is their favorite problem of the year.
Students used pennies, nickels, dimes and quarters to replicate the Tower of Hanoi. First, they started by solving an easier problem. What if, instead of 64 disks, there was only one disk? How many moves would be required to solve the problem? What if there were two disks? Three disks? From there, students saw patterns, formulated hypotheses, and tested their ideas.
They enjoyed the hands-on nature of the problem and appreciated the challenge of deriving an explicit formula to model the minimum number of moves to solve the Tower. They were curious as to whether there are extensions to the Tower (there are). Someone suggested that students create their own Tower extensions based on certain conditions (e.g. the Adjacency Requirement and double the original number of disks). Another Fellow saw how this problem could be modified for her students. A STEM coach, who knew of the problem prior to today, appreciated the problem solving approach using the coins, trial-and-error, patterns in the numbers and teamwork.
The Tower of Hanoi is the capstone activity of our Exponents unit. On day one of the Tower, students investigate a variation of the famous Wheat and Chessboard fable. On day two, they read the history of the Tower and attempt to solve it. Students are astounded by the number of years it would take, moving one disk per one second, to solve the Tower by hand. Day three offers extensions to the problem, including the Adjacency Requirement and Double Tower. Past students have told me that this is their favorite problem of the year.