ImagineIT Update #1
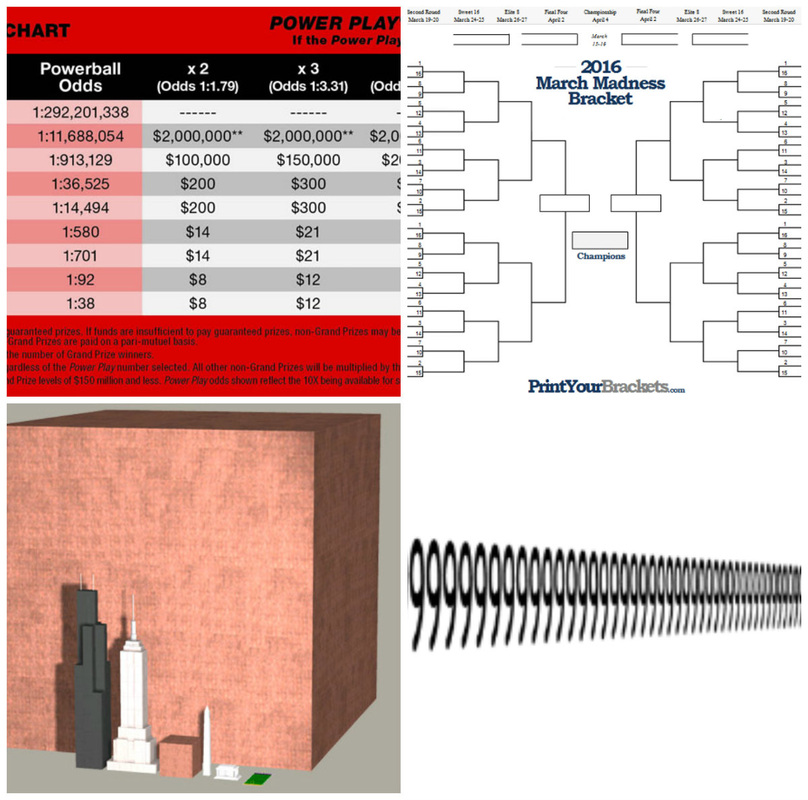
Before I dive into the update since the ImagineIT timeline was posted, it’s worth adding something that was omitted from the last assignment. In January, I had a week-long discussion with students about Powerball and the chances of winning the jackpot. This piqued student interest as the prize rose north of $1.5B. Discussing exceptionally large real numbers, and what it means to have a 99.99999966% of not winning the jackpot, did not convince all students that buying a Powerball ticket was a waste of money – but it did lead to an interesting debate. I followed up with a proposal designed to get kids to appreciate the magnitude of a mere 1,000,000: they were tasked with writing all of the whole numbers, from 1 to 1,000,000, on notebook paper. They had a month to do so, and I would pay $50 to any successful student. We discussed the impossibility of completing this task by hand by running the numbers (they’d have to write 33,333 numbers per day, 1389 numbers each hour, 23 numbers each minute and would earn around $0.07 per hour if the task was completed). These discussions have furthered my ImagineIT project on real numbers, even though they arose organically, not intentionally.
This past week, which followed an intense two week review and final exam period, was the first of the new semester. I was trying to get my bearings with new students and new material, so while I haven’t yet shown Dekofsky’s ‘The Infinite Hotel Paradox,’ I plan to do so before month’s end. Following quizzes in all of my classes next week, I plan to ask students to write a paragraph or draw a picture about whether they think 1=0.999… . The Two Balloons project is something I plan to implement after students complete a unit on systems of equations. Last week, we solved systems by graphing and substitution. This week will be spent on the elimination method and an assessment. The following week will include one or two days on Two Balloons.
A thought that’s arisen since my last post is one of my favorite segments of the year. I fleshed this out last year, and plan to build on it again this year: the number of ways a March Madness bracket can be completed. While we won’t necessarily be working with exponential functions in March, I think I can justify a mini-lesson on this (perhaps on a Friday). I’ll ask students, simply, how many ways do they think there are to complete an NCAA bracket with 64 teams selected? That the solution is nearly impossible to imagine – there are over 9.223 quintillion possible ways to complete a 64-team bracket – will help my students attempt to understand the true vastness of the RNL.
This past week, which followed an intense two week review and final exam period, was the first of the new semester. I was trying to get my bearings with new students and new material, so while I haven’t yet shown Dekofsky’s ‘The Infinite Hotel Paradox,’ I plan to do so before month’s end. Following quizzes in all of my classes next week, I plan to ask students to write a paragraph or draw a picture about whether they think 1=0.999… . The Two Balloons project is something I plan to implement after students complete a unit on systems of equations. Last week, we solved systems by graphing and substitution. This week will be spent on the elimination method and an assessment. The following week will include one or two days on Two Balloons.
A thought that’s arisen since my last post is one of my favorite segments of the year. I fleshed this out last year, and plan to build on it again this year: the number of ways a March Madness bracket can be completed. While we won’t necessarily be working with exponential functions in March, I think I can justify a mini-lesson on this (perhaps on a Friday). I’ll ask students, simply, how many ways do they think there are to complete an NCAA bracket with 64 teams selected? That the solution is nearly impossible to imagine – there are over 9.223 quintillion possible ways to complete a 64-team bracket – will help my students attempt to understand the true vastness of the RNL.